Authors: Dražen Adamović, Victor G Kac, Pierluigi Möseneder Frajria, Paolo Papi, Ozren Perše
International Mathematics Research Notices, rny237,
Abstract: We discover a large class of simple affine vertex algebras  , associated to basic Lie superalgebras
, associated to basic Lie superalgebras  at non-admissible collapsing levels
at non-admissible collapsing levels 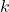 , having exactly one irreducible
, having exactly one irreducible  -locally finite module in the category
-locally finite module in the category  . In the case when
. In the case when  is a Lie algebra, we prove a complete reducibility result for
is a Lie algebra, we prove a complete reducibility result for  -modules at an arbitrary collapsing level. We also determine the generators of the maximal ideal in the universal affine vertex algebra
-modules at an arbitrary collapsing level. We also determine the generators of the maximal ideal in the universal affine vertex algebra  at certain negative integer levels. Considering some conformal embeddings in the simple affine vertex algebras
at certain negative integer levels. Considering some conformal embeddings in the simple affine vertex algebras  and
and  , we surprisingly obtain the realization of non-simple affine vertex algebras of types
, we surprisingly obtain the realization of non-simple affine vertex algebras of types  and
and  having exactly one nontrivial ideal.
having exactly one nontrivial ideal.
